数据
| t | N |
|---|---|
| 1790 | 3929 |
| 1800 | 5308 |
| 1810 | 7240 |
| 1820 | 9638 |
| 1830 | 12866 |
| 1840 | 17069 |
| 1850 | 23192 |
| 1860 | 31443 |
| 1870 | 38558 |
| 1880 | 50156 |
| 1890 | 62948 |
| 1900 | 75995 |
| 1910 | 91972 |
| 1920 | 105711 |
| 1930 | 122775 |
| 1940 | 131669 |
| 1950 | 150697 |
| 1960 | 179323 |
| 1970 | 203185 |
| 1980 | 226500 |
令:
$$
N_0=3929,t_0=1790
$$
训练集:
N1=N(1:10,1)
t1=t(1:10,1)
测试集:
N2=N(11:20,1)
t2=t(11:20,1)
Malthusian模型
$$
\frac{dN}{dt}=rt
\Rightarrow\ln{\frac{N}{N_0}}=r(t-t_0)
$$
采用最小二乘法:
A=(t1-1790);
b=log(N1/3929);
r=inv(A'*A)*A'*b;
f=3929*exp(r*(t-1790))
scatter(t1,N1)
hold on
scatter(t2,N2)
plot(t,f)
legend({'train','test','fit'},'Location','northeast')
得:$$r=0.029$$
可视化结果:
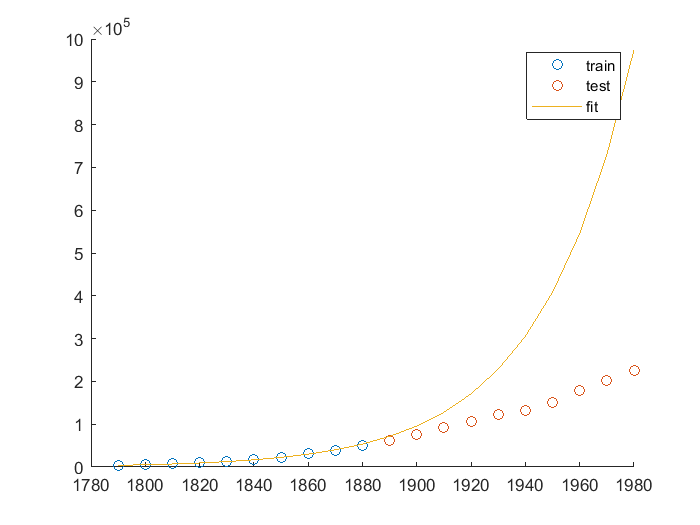
可视化结果已证实该模型严重不合实际,无需进一步验证。
Logistic模型
$$
\frac{1}{N}\frac{dN}{dt}=r(1-\frac{\bar{N}}{N})
\Rightarrow N=\frac{\bar{N}}{1+(\frac{\bar{N}}{N_0}-1)e^{-r(t-t_0)}}
$$
采用等时间间隔四点法:
A=N1(1,1);
B=N1(5,1);
C=N1(6,1);
D=N1(10,1);
M=(A*D*(B+C)-B*C*(A+D))/(A*D-B*C);
X=t1-1790;
r=inv(X'*X)*X'*-log((M./N1-1)/(M/3929-1));
f=M./(1+(M/3929-1)*exp(-r*(t-1790)));
scatter(t1,N1)
hold on
scatter(t2,N2)
plot(t,f)
legend({'train','test','fit'},'Location','northeast')
得:$$r=0.0306,\bar{N}=265159.887893331$$
可视化结果:
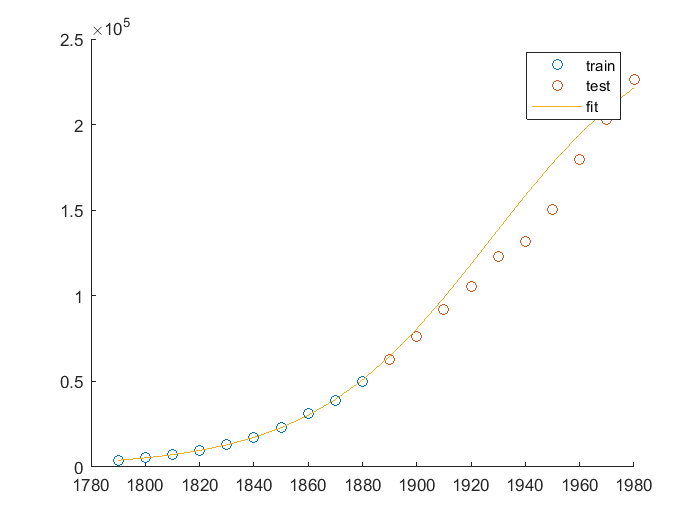
可视化效果良好,可进一步验证。
R-square:
>> 1-sum((f1-N1).^2)/sum((N1-mean(N1)).^2) # 训练集
ans =
0.9987
>> 1-sum((f2-N2).^2)/sum((N2-mean(N2)).^2) # 测试集
ans =
0.9167
F检验:
>> [h,p] = vartest2(f1,N1)
h =
0
p =
0.9770
>> [h,p] = vartest2(f2,N2)
h =
0
p =
0.9850
以上结果均表明较好拟合优度。